A linked list is a data structure that holds objects arranged in a linear order, this order is determined by a pointer in each node. Unlike an array, a linked list doesn't provide constant-time access to a particular index, you have to iterate through the list to find an element, on the other hand, is possible to add and remove items from the beginning of the list in a constant time. Linked lists can be used to implement other data structures, such as stacks, queues, and graphs.
There are some types of linked lists:
- Singly linked list - Each node has only a pointer to the next node.
- Doubly linked list - Each node has pointers to both the previous and next node.
- Circular linked list - The last node points to the first element.
Representation
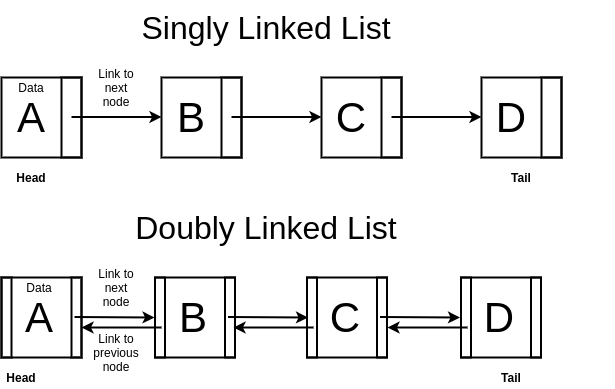
- Head - the first node
- Tail - the last node
Basic operations
Insertion - It's possible to insert a new element anywhere in the list, you just have to take care of the pointers. If you are adding an element to the beginning the new node will pointer to the former head node. If you are appending to the tail, the former tail node will point to the new node. Now, if inserting between nodes, the previous node has to point to the new node which will point to the next node
Deletion - Follow a similar logic of insertion, if you want to remove a node from the middle of the list, you just have to make the target's previous node point to the target's next node. In a doubly-linked list, you have to take care of the previous pointer too.
Traverse - Each node has a point to next, so you start from the node head and follow the pointers until the last node, which will not point to any node (in a non-circular linked list)
1n = list.head 2 3while n != null 4 n = n.next 5
Here's an implementation of a singly linked list:
1class Node<T> {
2 data: T;
3 next: Node<T> | null = null;
4
5 constructor(data: T) {
6 this.data = data;
7 }
8}
9
10class LinkedList<T> {
11 head: Node<T> | null = null;
12 comparator: (a: T, b: T) => boolean;
13
14 constructor(comparator: (a: T, b: T) => boolean) {
15 this.comparator = comparator;
16 }
17
18 append(data: T): void {
19 if (!this.head) {
20 this.head = new Node(data);
21 } else {
22 let current = this.head;
23 while (current.next != null) {
24 current = current.next;
25 }
26 current.next = new Node(data);
27 }
28 }
29
30 delete(data: T): void {
31 if (!this.head) return;
32
33 // Check if the head node is the node to be removed
34 if (this.comparator(this.head.data, data)) {
35 this.head = this.head.next;
36 return;
37 }
38
39 let current = this.head.next;
40 let previous = this.head;
41
42 /**
43 * Search for the node to be removed and keep track of its previous node
44 *
45 * If it were a double linked list, we could simply search the node
46 * and it would have a pointer to the previous node
47 **/
48 while (current) {
49 if (this.comparator(current.data, data)) {
50 current = null;
51 } else {
52 previous = current;
53 current = current.next;
54 }
55 }
56
57 /**
58 * set previous.next to the target.next, if the node target is not found,
59 * the 'previous' will point to the last node,
60 * since the last node hasn't next, nothing will happen
61 **/
62 previous.next = previous.next ? previous.next.next : null;
63 }
64
65 search(data: T): Node<T> | null {
66 let current = this.head;
67 while (current) {
68 if (this.comparator(current.data, data)) {
69 return current;
70 }
71 current = current.next;
72 }
73 return null;
74 }
75
76 traverse() {
77 let current = this.head;
78 while (current != null) {
79 console.log(current.data);
80 current = current.next;
81 }
82 }
83}
Runner technique
This technique consists in iterate through a linked list with two pointers, a slow and a fast which will be ahead of the slow pointer by n nodes.
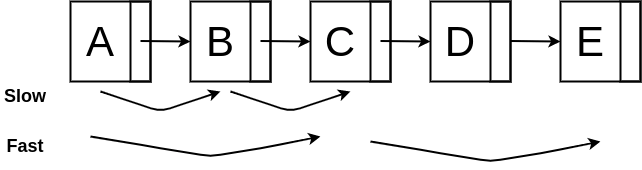
This is useful to solve some problems with a linked list, like detecting a cycle or finding the middle node of a linked list when you don't know its size.
1/** Finding the middle node of a linked list **/ 2 3let slow: LinkedListNode<number> | null | undefined = linkedList.head; 4let fast: LinkedListNode<number> | null | undefined = linkedList.head?.next; 5 6/** 7 * The "fast" will move twice as fast as the "slow" one, 8 * so at the moment the "fast" reaches the end of the list, 9 * the "slow" will be in the middle of the list 10 **/ 11 12while (fast) { 13 slow = slow?.next; 14 fast = fast?.next?.next; 15} 16 17console.log(slow);

